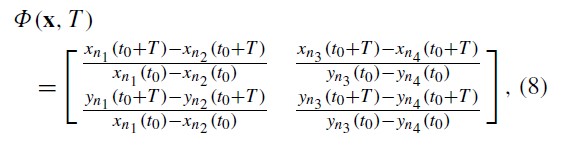Mathematical modeling, computational modeling, and simulations are powerful tools that can be used to characterize a complex system. They may be used to model an existing system to enhance our understanding of its behavior including the strength of an engineering structure, leaching from an implanted medical device, or cellular migration characteristics. They can also be used to simulate something new that is being considered such as potential outcomes of different surgical options or chemotherapy strategies.
They can be used to conduct “virtual experiment” that run in seconds and at minimal cost compared with physical experiments that often require weeks or months to conduct. They can even be used to evaluate potential outcomes for instances where it is unethical to perform actual experiments such as the transmission of diseases like COVID-19, the effects of protections like masks and social distancing, and the number of deaths based on the approach taken.
NSF/FDA Scholar in Residence: Histomorphogenesis and Phase Field Models
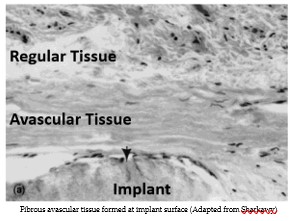
The original project examined leaching from an implanted medical device over the period of 24 hours following implantation. This new study examines long term exposure and changes to tissue properties during the healing process.
- Research was performed in collaboration with scientists and engineers at the US Food and Drug Administration (FDA) with the goal of developing better methods for the evaluation of medical devices.
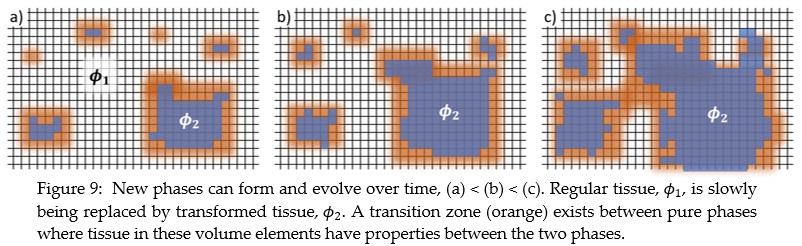
- Changes to tissue properties that occur during healing are considered in the model (histomorphogenesis).
- Phase field models will be used to simulate the two tissue types, normal tissue and fibrous avascular tissue that encapsulates an implanted medical device.
- Predictive models can reduce development cost, decrease animal testing, and enable products to reach the market faster without sacrificing public protection.
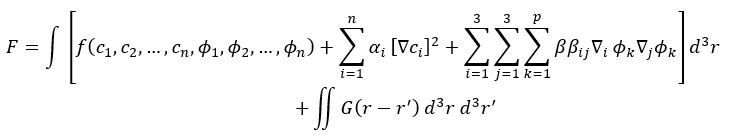
Cell Migration Modeling
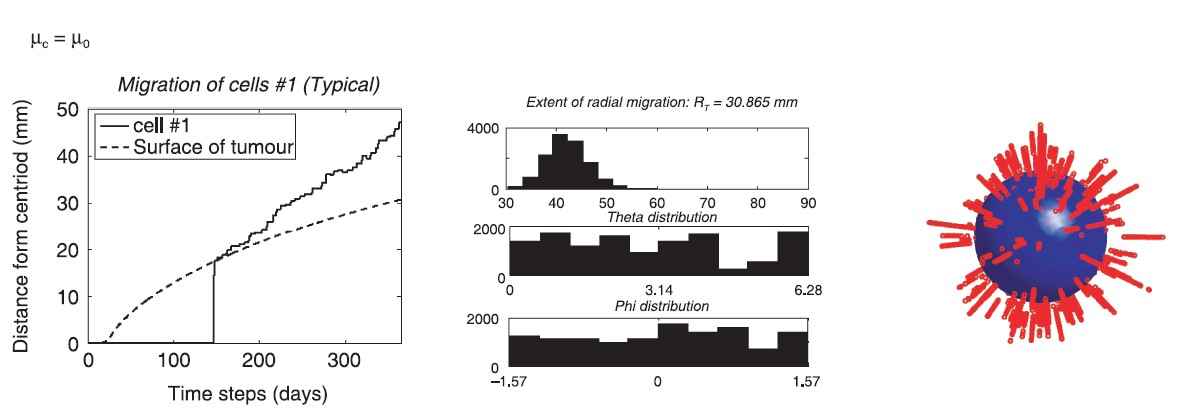
Computational models can be used to characterize the movement of cells in artificial tissue used to repair damage cause by injury, osteoarthritis, or cancer. Mesenchymal stem cells are cells that every person has in their body to repair damaged tissue. In regenerative medicine, we would like these cells the “crawl” into the engineered tissue and differentiate into chondrocytes that produce the cartilage and maintain the extracellular matrix.
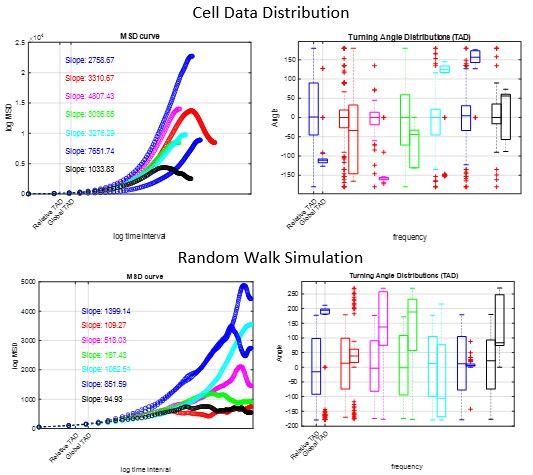
Two research projects are ongoing. The first is to obtain cell movement characteristics through the analysis of video data. Characteristics of interest include cell velocities, cell diffusion rates, and trajectory persistence. The second is to characterize the cellular dispersion using differential equations, random walks, and drifts. These models will use model parameters found in the literature and those discovered in the first research project. We hope to use this information to provide insight into experimental studies and to inform future experiments to develop better artificial tissues more quickly for articular cartilage repair.
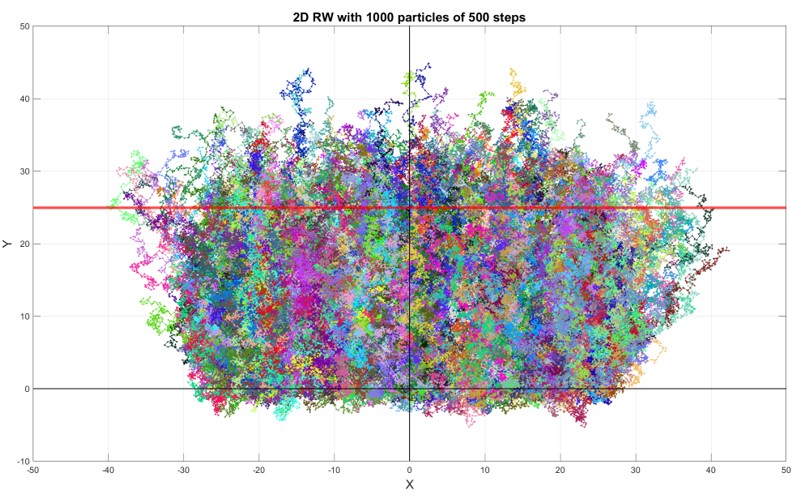
NSF/FDA Scholar in Residence: Polymer-Interface-Tissue Models
Computer models were developed to estimate exposure to potentially hazardous materials released from an implanted medical device.
- Research was performed in collaboration with scientists and engineers at the US Food and Drug Administration (FDA) with the goal of developing better methods for the evaluation of medical devices.
- Chemicals contained within an implanted medical device can pose a risk to human health if they migrate into surrounding tissues.
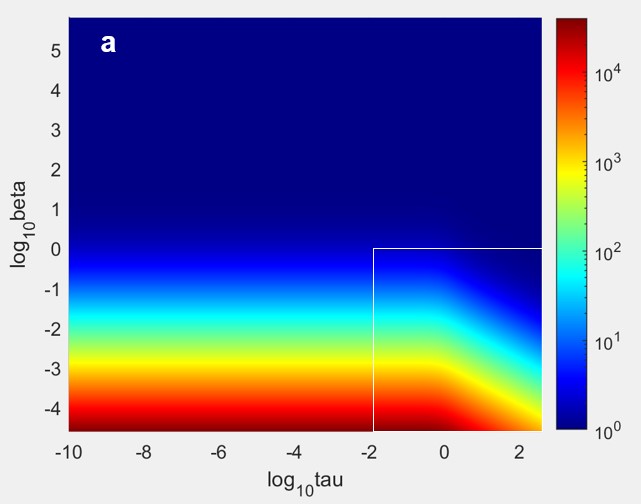
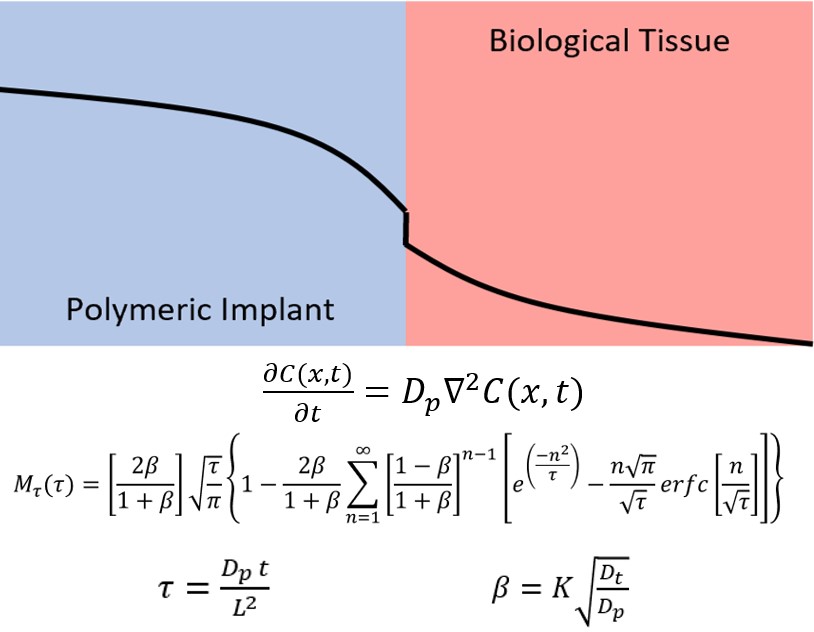
- Computer simulations were developed for a new, more clinically relevant model that included the polymeric implant, the implant tissue interface, and the surrounding tissue.
- Model behavior was analyzed over the typical range of input parameter values to understand the influence of different size devices, different polymer types, different leachable materials, and different tissues.
- When results were compared to existing models, up to a 4,500 times difference in mass release was found using the more clinically relevant model for some input parameter values.
- Predictive models can reduce development cost, decrease animal testing, and enable products to reach the market faster without sacrificing public protection.
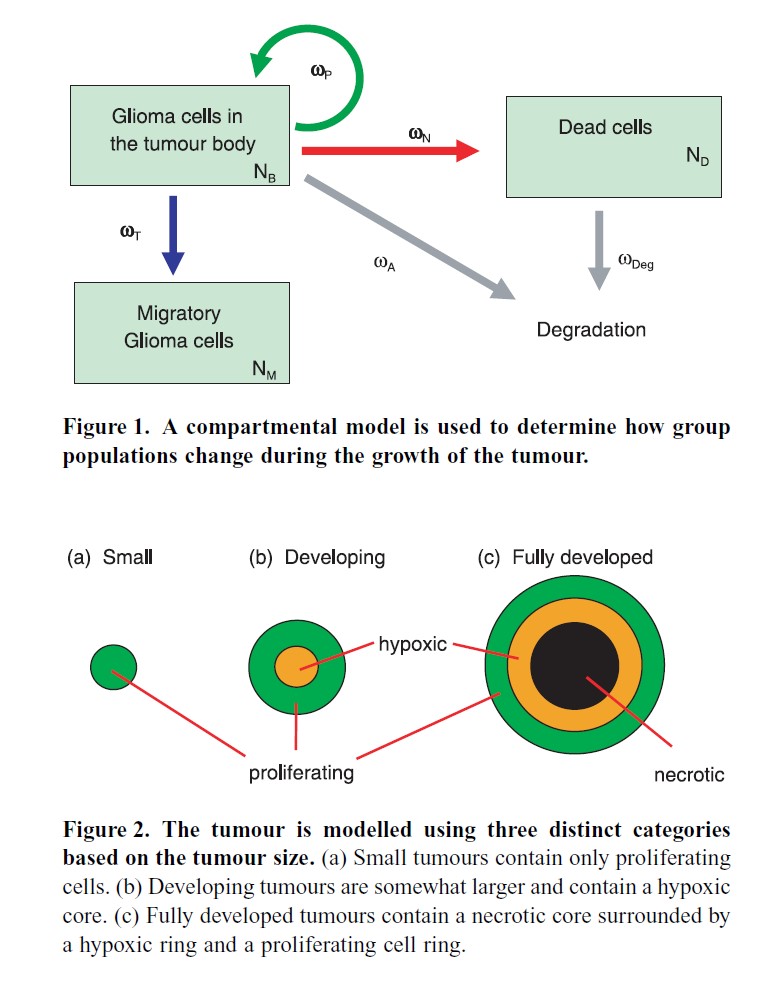
Brain Tumor Modeling: Tracking GBMs
Primary brain tumors are among the most aggressive and lethal forms of cancer, with gliomas being the most prevalent. Gliomas are derived from transformed glial cells and account for 30–40% of all primary intracranial neoplasms. The most common and lethal are glioblastoma multiforme (GBM), a World Health Organization grade IV astrocytoma.
Mathematical models are often used to understand and predict their behavior. However, using traditional modeling techniques one must choose between simulating individual cell behavior and modeling tumors of clinically significant size.
We developed a hybrid compartment-continuum-discrete model to simulate glioma growth and malignant cell invasion. The discrete portion of the model can capture intercellular interactions, such as cell migration, phenotype differentiation, epigenetic events, proliferation, and apoptosis. Combining this with a compartment and continuum model allows tumors of clinically significant size to be evaluated.
Multiple simulations were executed to determine the sensitivity to changes in important model parameters, including the fundamental length parameter, necrotic cell degradation rate, rate of cell migration, and rate of phenotype transformation. Through adjustment of these parameters, the model can simulate tumor growth and invasion behavior observed clinically.

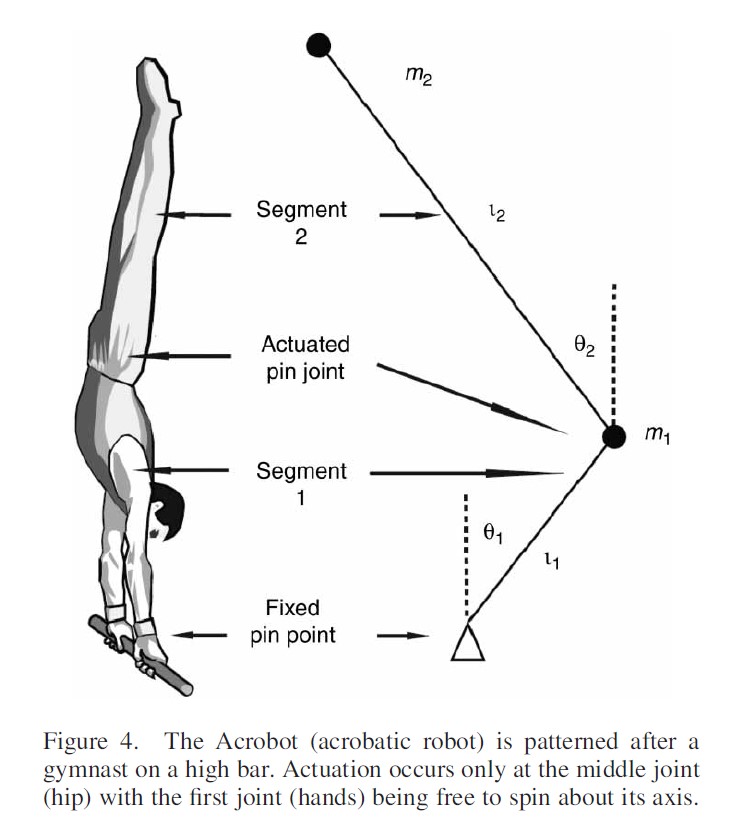
Using Topological Equivalence to Achieve System Stability
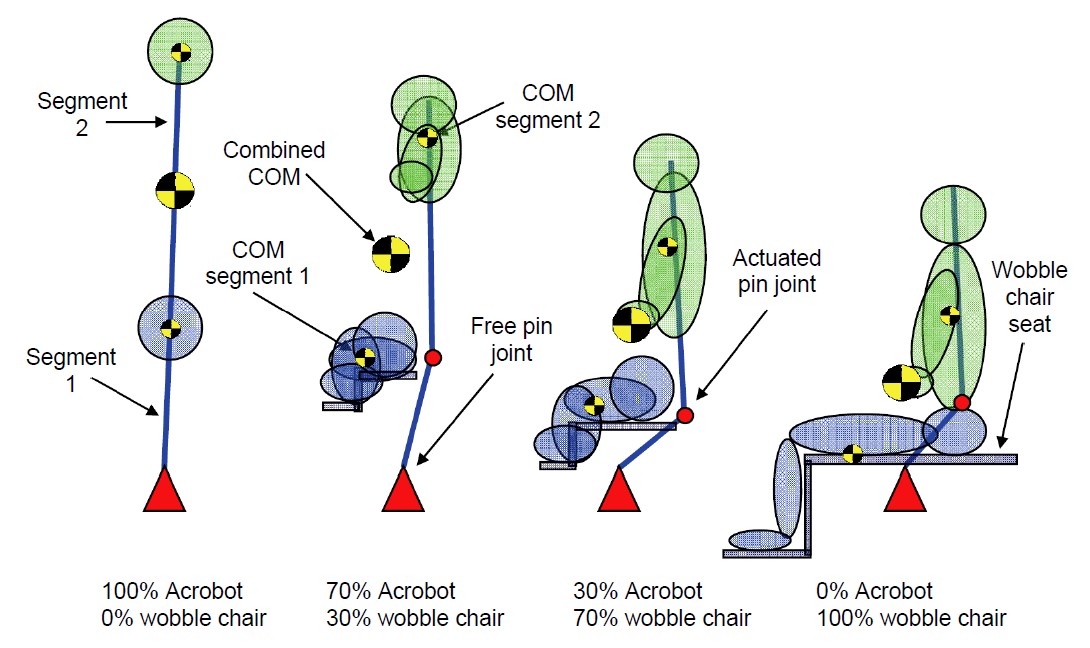
Low back pain is the leading form of disability in the USA affecting 4 of 5 people at some point in their life. To better understand the mechanisms that contribute to low back pain, a computational model that included human geometry and neuromuscular feedback control was developed to simulate a person balancing on an unstable sitting apparatus, the wobble chair.
When the direct method failed to discover suitable controller gain parameters, we show how topological equivalence was used to solve the problem. The solution was found by first transforming the wobble chair into the Acrobot, a topologically equivalent dynamical system. After finding controller gain parameters that stabilized the system, a continuous transformation was performed to convert the Acrobot back to the wobble chair, during which the gain parameters were adjusted to maintain stability. Thus, we demonstrate how topological equivalence can be used to indirectly solve a problem that we could not solve directly.
Note: The wobble chair and Acrobot do not have an actuator connecting the first segment to the based, thus they are underactuated. Because the Acrobot had a larger range of controller gain parameters that showed stable behavior it was easier to solve. Once solved, the parameters could be adjusted to also solve for the wobble chair which had a much smaller window for stability.

Locating Lagrangian Coherent Structures in Time Series Data
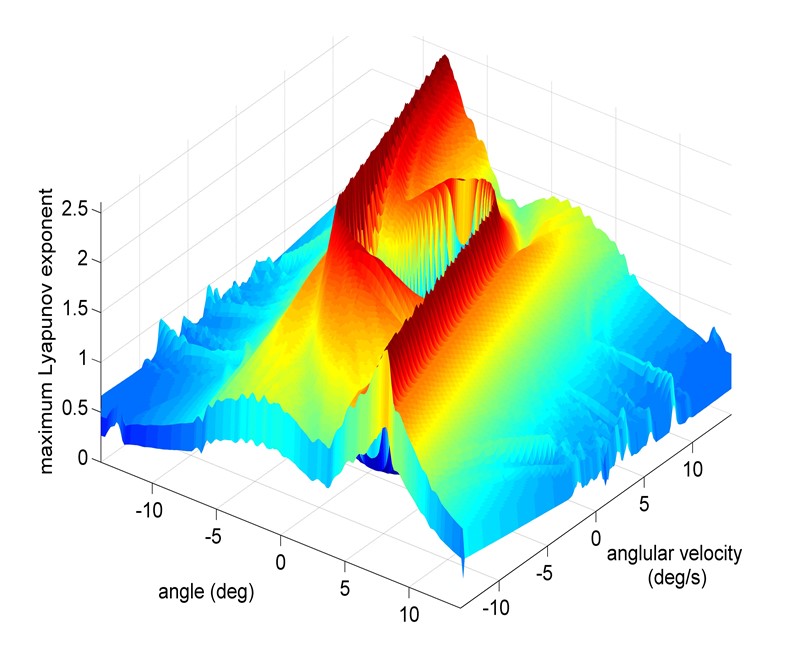
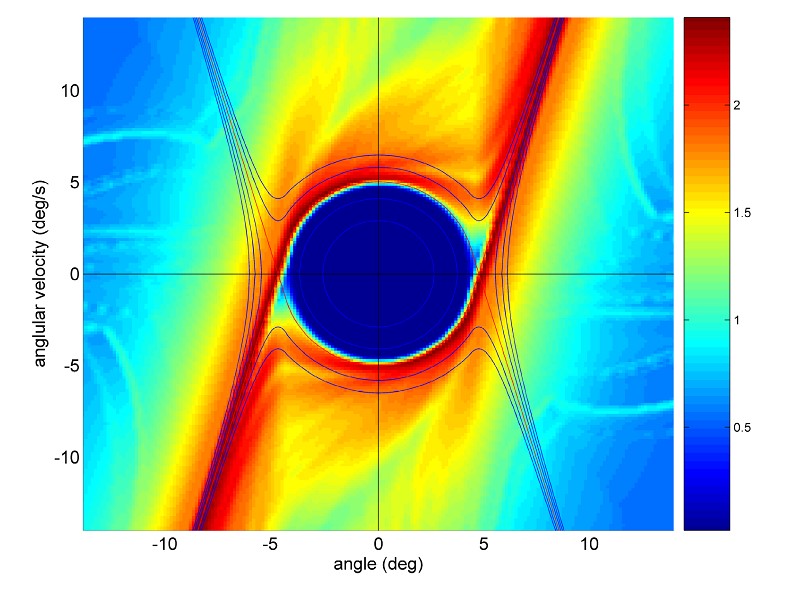
Ridges in the state space distribution of finite-time Lyapunov exponents can be used to locate dynamical boundaries. We describe a method for obtaining dynamical boundaries using only trajectories reconstructed from time series, expanding on the current approach which requires a vector field in the phase space.
We analyze problems in musculoskeletal biomechanics, considered as exemplars of a class of experimental systems that contain separatrix features. Particular focus is given to postural control and balance, considering both models and experimental data.
Our success in determining the boundary between recovery and failure in human balance activities suggests this approach will provide new robust stability measures, as well as measures of fall risk, that currently are not available and may have benefits for the analysis and prevention of low back pain and falls leading to injury, both of which affect a significant portion of the population.
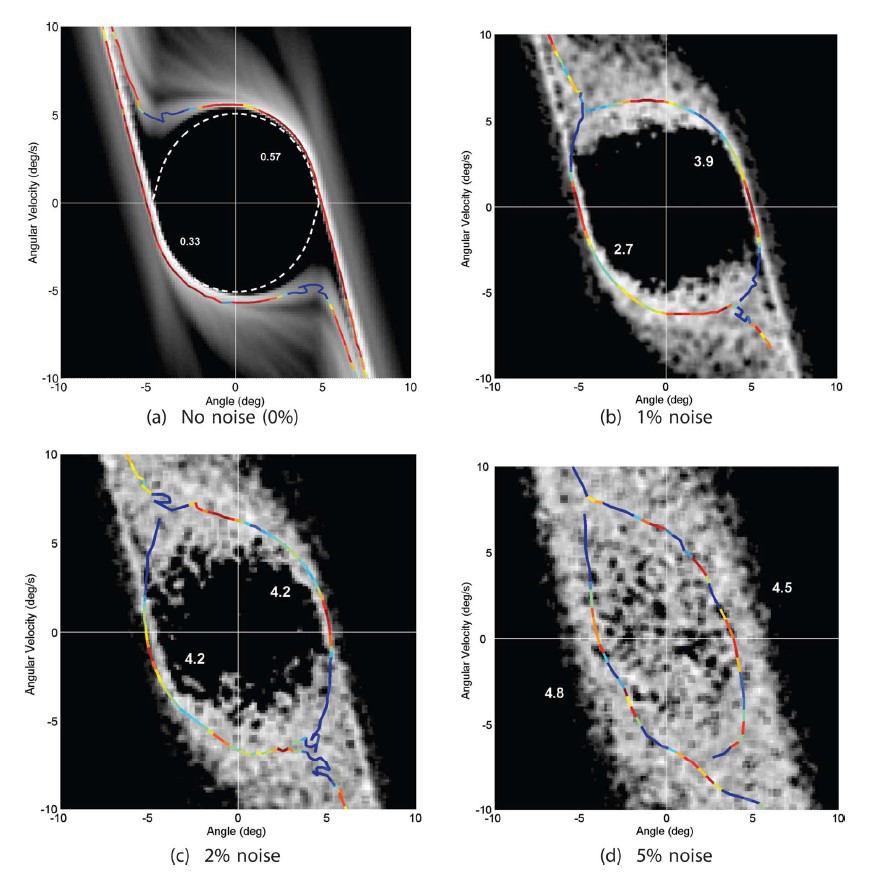

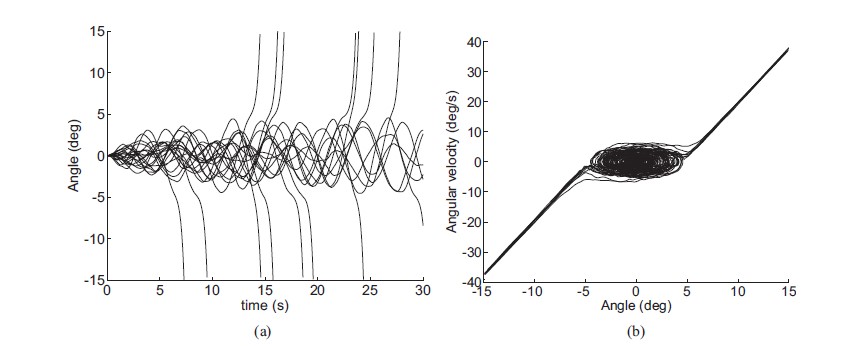
Separatrices and Basins of Stability in Biodynamics
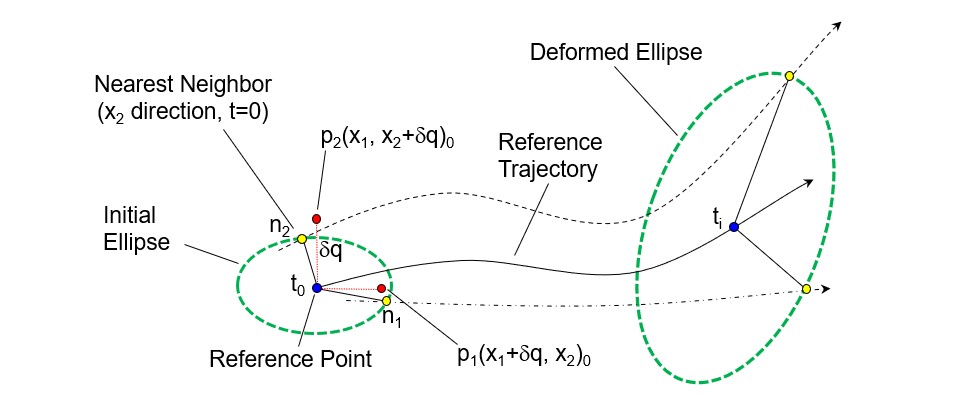
An approach is presented for identifying separatrices in state space generated from noisy time series data sets which are representative of those generated from experiments. We demonstrate how these separatrices can be found using Lagrangian coherent structures (LCSs), ridges in the state space distribution of the maximum finite-time Lyapunov exponent.
As opposed to traditional approaches which require a vector field in state space at each instant of time, this method can be performed using only trajectories reconstructed from time series. As such, this research forms a bridge connecting methods for evaluating time series data with methods used to evaluate LCSs in vector fields.
The methods are applied to a problem in musculoskeletal biomechanics, considered as an exemplar of a class of experimental systems that contain separatrices. In this case, the separatrix reveals a basin of stability for a balancing task, outside of which is a zone of failure.
We demonstrate that LCSs calculated from only trajectory data, which samples only portions of the state space, align well with LCSs found using a known vector field. In general, we believe this method provides a fruitful approach for extracting information from noisy experimental data regarding boundaries between qualitatively different kinds of behavior.